↜ Back to index Introduction to Numerical Analysis 1
Solution Lecture a5
Exercise 1
! Implementation of the midpoint method for the system y_1' = y_2, y_2' = - sin(y_1)
implicit none
integer i, n
real h, t
real y(2), k(2)
real pi, theta0
read *, theta0, h
n = 20 / h
! Initial data
y = [theta0, 0.]
print *, 0., y
do i = 1, n
k = y + 0.5 * h * [y(2), -sin(y(1))]
y = y + h * [k(2), -sin(k(1))]
print *, i * h, y
enddo
end1.
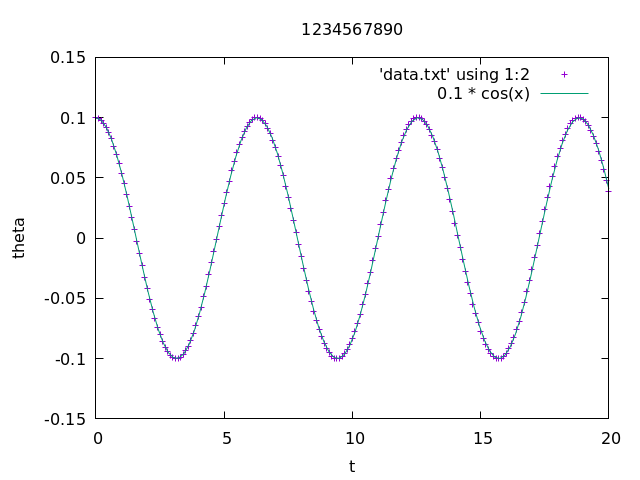
2.
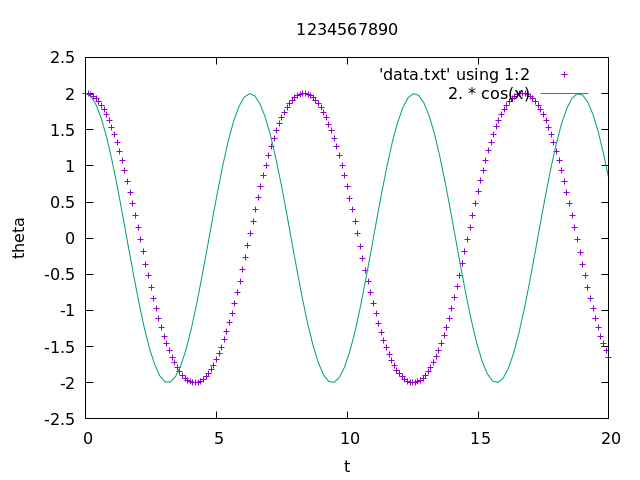
3.
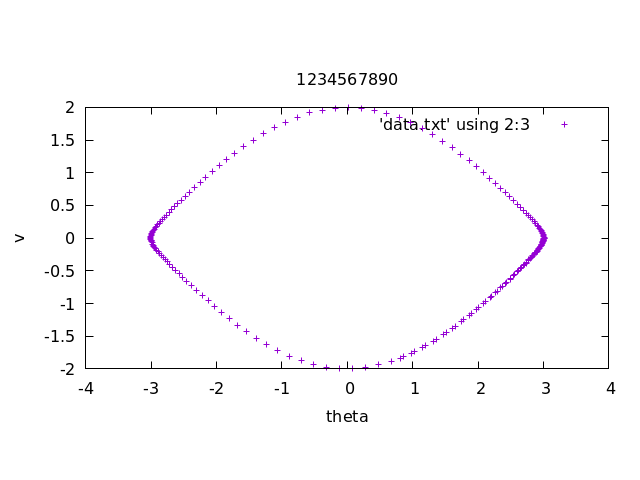
Exercise 2
! Finding the period of a physical pendulum
implicit none
integer i, j, n
real h
real y(2), k(2)
real theta0
h = 0.001
! let's assume that the period is < 100 * 4
n = 100 / h
do j = 1, 30
theta0 = j * 0.1
y = [theta0, 0.]
do i = 1, n
! midpoint method
k = y + 0.5 * h * [y(2), -sin(y(1))]
y = y + h * [k(2), -sin(k(1))]
if (y(1) <= 0.) then
! 👇 period
print *, theta0, 4. * i * h
exit
endif
enddo
enddo
end